Actividad de Aprendizaje No. 2: Selección de Vistas

Actividad de Aprendizaje No. 1 

SISTEMAS DE REPRESENTACIÓN Y VISTAS NORMALIZADAS

Antes de comenzar, hemos de recordar que nuestro objetivo básico es plasmar sobre un papel una pieza o un conjunto de piezas de la forma más clara posible.

Dicha información ha de ser transmitida de una a otras personas de manera eficaz, desde los ingenieros proyectistas hasta las personas encargadas de su ejecución física: al fin y al cabo, los planos de dibujo van a ser los documentos con los que habremos de comunicarnos y transmitir datos técnicos.

Por consiguiente, debe conocerse por todas las partes implicadas la forma correcta de representación de una pieza (“vistas” de pieza). La representación gráfica de una pieza cualquiera ha de realizarse mediante dichas vistas, siempre de manera que el plano resulte preciso, completo y no ofrezca más de una interpretación posible.

No obstante, los planos deberán ir acompañados por lo general de la indicación de sus dimensiones (“acotación”), ciertos datos necesarios para su fabricación y una serie de símbolos normalizados que detallaremos ampliamente en posteriores capítulos.

Es evidente que, si además de realizar dicha representación de forma completa, consigue hacerlo de la manera más sencilla posible para futuras interpretaciones, habrá realizado sin duda un buen trabajo. Por todo ello es necesario que tanto el creador como el intérprete del plano conozcan los diferentes sistemas de distribución de las vistas y su aplicación, lo que redundará en la determinación de las vistas estrictamente necesarias.

sistemas de representación

Todos los sistemas de representación creados por el hombre se hallan basados en las diferentes formas de proyección planteadas.

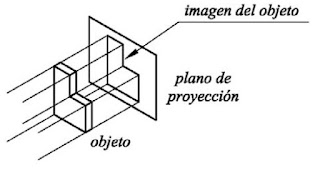
”Proyectar” un punto o una recta consiste en “lanzar” imaginariamente un punto o una línea sobre un plano de proyección, lo que dicho de otro modo supone la representación sobre dicho plano de los vértices y aristas que componen el cuerpo que se desea representar sobre el papel.

Hablando en términos más precisos, llamaremos “proyección” de un punto sobre un plano a la intersección entre el citado plano y la línea resultante de la proyección del punto en cuestión. Las diferentes clases de proyección existentes se resumen del siguiente modo:

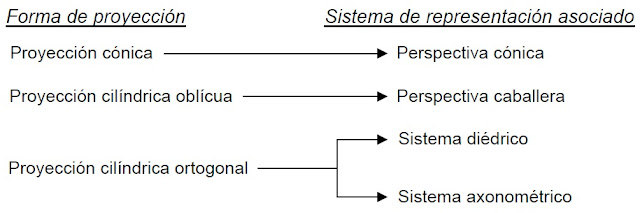
Proyección cónica: cuando todas las líneas de proyección (también llamadas “rayos de proyección”) coinciden en un mismo vértice de proyección o punto de vista.

Proyección cilíndrica ortogonal: cuando todas y cada una de las líneas de proyección son paralelas entre sí y perpendiculares a un plano de proyección.

Proyección cilíndrica oblicua: cuando todas y cada una de las líneas de proyección son paralelas entre sí y oblicuas a un plano de proyección. Para una mejor comprensión se ha procedido a incluir en el siguiente gráfico explicativo un detalle del resultado de las proyecciones de dos puntos A y B cualesquiera de la figura representada.

CLASES DE SISTEMAS DE REPRESENTACIÓN

En el apartado anterior hemos recordado los diferentes sistemas de proyección.

Lógicamente, según la forma de proyectar escogida obtendremos también distintos sistemas de representación. Resumimos a continuación los más importantes:

PERSPECTIVA CÓNICA

La perspectiva cónica podría ser definida como aquella que permite la representación del objeto tal y como se ve, y no como es en la realidad. Aunque parezca un juego de palabras, lo cierto es que el ojo humano tiene un campo visual (también llamado “apertura” del horizonte) de tan sólo 60º, y es por ese motivo precisamente por lo que debemos separarnos una distancia mínima del objeto para poder visualizarlo de forma completa.

Pongamos un ejemplo: todos sabemos que una vía de ferrocarril está formada por unas traviesas y por dos raíles paralelos entre sí. Sin embargo, tanto el ojo humano como observando una fotografía visualiza los raíles “juntándose” en un punto lejano del horizonte

Por este motivo no tiene sentido hablar de coeficientes de reducción en esta perspectiva, puesto que conforme aumenta la lejanía del objeto, la percepción en cuanto a disminución de longitud aumenta gradualmente (no puede asignarse un valor numérico concreto).

Recordaremos rápidamente que la perspectiva cónica intenta simular este modo de visualizar los objetos, pudiéndose encontrarse dos tipos, la “perspectiva cónica frontal” y la “perspectiva cónica oblicua”.

PERSPECTIVA CÓNICA FRONTAL

En este tipo de perspectiva, el objeto se sitúa paralelo al plano del cuadro, de tal forma que existe un único punto de fuga (punto donde concurren todas las líneas de proyección) y de vista, por lo que ambos resultan ser el mismo punto.

PERSPECTIVA CÓNICA OBLICUA

En este otro caso, el objeto visualizado no tiene ningún lado paralelo al plano que sirve de fondo; por este motivo encontraremos dos puntos de fuga, que no coinciden con el punto de vista.

Dada la relativamente escasa aplicación en el dibujo técnico industrial, no insistiremos más sobre este particular y nos centraremos en modos de representación más adecuados para nuestros propósitos.

La perspectiva cónica se trata de un tipo de realización que encuentra una mayor aplicación en el campo de las artes gráficas, diseño, etc., que en el dibujo puramente industrial.

PERSPECTIVA CABALLERA

La proyección cilíndrica oblicua sienta las bases de la perspectiva caballera, también denominada perspectiva rápida.

En este tipo de perspectiva, las líneas proyectantes, son paralelas entre sí pero resultan oblicuas al plano de proyección, por lo que no debe confundirse con la perspectiva axonométrica (en la que las líneas de proyección resultan paralelas entre sí y perpendiculares al plano de proyección).

La perspectiva caballera es ampliamente utilizada, y resulta especialmente en la realización de croquis.

Disposición de ejes

Como puede comprobarse en la figura, los ejes X y Z son perpendiculares, a 90º, y la vista que se representa sobre el plano XZ no resulta deformada, se representa con las dimensiones reales.

Sin embargo, el eje Y forma un determinado ángulo respecto del eje X, y es el encargado de dar la sensación de profundidad a la pieza. Por este motivo debemos aplicar un coeficiente de reducción (generalmente es denominado con el carácter “μ”) , para que las vistas plasmadas en los planos XY y YZ den dicha sensación: de no ser así y dibujar sin reducción en el eje Y, nos daría la sensación de estar visualizando una pieza más larga y consecuentemente deformada.

SISTEMA DIÉDRICO

El sistema diédrico está basado en proyecciones ortogonales sobre los planos de proyección, es decir, las líneas de proyección son paralelas entre sí y perpendiculares al plano de proyección.

Cada una de las proyecciones ortogonales que se realice de un objeto sobre los planos de proyección forma lo que conocemos bajo el nombre de “vistas” de una pieza. Son con dichas vistas y una correcta acotación, reflejadas sobre el papel en 2D, como interpretaremos habitualmente la forma y dimensiones de una pieza.

El modo de proyectar y posicionar sobre el plano cada uno de los vértices y aristas que componen el objeto a representar sigue una serie de normas preestablecidas, pero dada su importancia se tratará detalladamente en un posterior apartado.

SISTEMA AXONOMÉTRICO

En la perspectiva axonométrica las líneas de proyección son paralelas entre sí y son perpendiculares al plano de proyección, pero el objeto se halla “girado” con relación al plano del dibujo. 

Tenga en cuenta de que si el objeto no estuviese girado, y las líneas de proyección fuesen paralelas entre sí y perpendiculares al plano de proyección, estaríamos ante una proyección cilíndrica ortogonal, base del sistema diédrico analizado anteriormente.

Las tres dimensiones del objeto resultan paralelas a los ejes X, Y, Z.

En esta perspectiva aparecerán las dimensiones de la pieza reducidas en cualquiera de los tres ejes, por lo que habrá que aplicar de nuevo un coeficiente de reducción, esta vez a los tres ejes considerados.

Tipos de perspectiva axonométrica

Según la inclinación que presente cada eje respecto al plano del dibujo, tendremos tres tipos de perspectiva axonométrica, y que son:

Perspectiva isométrica: 

Los tres ejes X, Y, Z quedan posicionados a 120º y forman tres ángulos iguales (α = β = γ)

Perspectiva dimétrica: 

Los tres ejes forman dos ángulos iguales y uno desigual (α ≠ β = γ) o (γ ≠ α = β).

Perspectiva trimétrica: 

Los tres ejes forman tres ángulos desiguales (α ≠ β ≠ γ).

Sin lugar a dudas, es la perspectiva axonométrica isométrica (denominada comúnmente “isométrica”), la más utilizada por su facilidad de manejo en numerosas ocasiones; sin embargo no puede decirse lo mismo de las otras dos perspectivas axonométricas, por lo que no insistiremos más sobre ellas.

En la perspectiva isométrica los tres ejes X, Y, Z se posicionan a 120º, por lo que en los tres ejes debe aplicarse el mismo coeficiente de reducción.

El coeficiente de reducción a aplicar es siempre μ=0,816, es decir, se reducen las dimensiones reales del objeto al 81%. Como curiosidad, indicaremos que 0,816 es el coseno del ángulo de 35º 16' que forma cada uno de los ejes con el plano del dibujo.